Based on a plenary talk presented at the 1996 Summer Meetings of the Econometric Society.
Drew Fudenberg and David K. Levine
June 26, 1996; revised July 30, 1996
This essay has two goals. First, it is an overview of the field to give
an idea of what has been going on recently. Second, it is an editorial for our own views
of how future research ought to proceed.
The basic research agenda is to explore non-equilibrium explanations of
equilibrium in games; to view equilibrium as the long-run outcome of a dynamic process of
adjustment or learning. In other words, equilibrium concepts should be interpreted as
steady states or ergodic distributions of a dynamic process. This essay focuses on
theoretical models of learning, but is informed by and addressed to experimenters as well,
and we have suggestions about how each group "ought" to proceed.
In our view, game theorists ought to pay more attention to game theory
experiments; for example, the literature on refinements of Nash equilibrium proceeded
based almost entirely on introspection and theoretical concerns. Laboratory experiments
may not be perfect tests of theories, but they are much better than no tests at all. Our
second message to theorists is that more attention should be paid to the "medium
run" properties of learning models: Most work, including our own, has focused on
asymptotic results, which tend to be easier to obtain.
Of course, any experiment in which subjects play more than one round at
least implicitly involves learning, and indeed most experiments focus on play in the last
few rounds of the experiment, when subjects have had the most time to learn. Given this
heavy implicit reliance on the idea of learning, we feel that experimenters ought to pay
more attention to the relevant learning theory. For example, a variety of learning models
have been studied by experimental economists without much concern for the extent to which
the models do a good job of learning. Although we are prepared to be convinced otherwise
by sufficiently strong data, our prior belief is that in environments where simple
learning rules can do well, agents will tend not to use rules that do poorly. For this
reason we are skeptical of claims that very simple models fit the data well unless those
models are compared with medium-complexity models that do a better job of learning.
From a theorist's perspective, there are three criteria for good
experiments: interesting questions, appropriate theoretical foundations, and careful
experimental design. In our opinion, too many experiments focus on careful experimental
design, changing only a few treatment variables from a past experiment in order to isolate
their effect, and too few experiments try to answer questions of theoretical interest. Of
course, this procedure is useful for identifying the reasons that outcomes differ between
the treatments, but we believe that more attention to theoretical issues would help
experimental economics move beyond laundry-lists of treatment effects in various games.
Instead of drawing a t distinction between models of "learning" and other forms of adjustment, it is easier to make a distinction between models that describe behavior of individual agents and those that start at the aggregate level. Consequently, the real taxonomy is not between "learning" and "evolutionary" models, but rather between "individual level" models and "aggregate" models. This essay focuses on individual level models, but we would like to make a few comments on aggregate models before we begin.
An aggregate model starts with a description of aggregate behavior of a
population of agents. An example of this is the "replicator dynamic" that
postulates that the fraction of the population playing a strategy increases if the utility
received from that strategy is above average. There are two main reasons that economists
are interested in the replicator and related models.
First, although the replicator dynamics was originally motivated by
biological evolution, it can be derived from various sorts of individual-level models. One
such model is the stimulus-response model of Borgers and Sarin [1994] which postulates
that actions that perform well are "positively reinforced" and so more likely to
be played in the future. An alternative model is the "emulation" model in which
players copy their more successful predecessor, as in Binmore and Samuelson [1995],
Bjonerstedt and Weibull [1995], or Schlag [1995]. Note, however, that the
"emulation" stories are not applicable to most experiments, because subjects are
not told what happens in other matches. These emulation models are very similar to
non-equilibrium models of "social learning," where players are trying to learn
what technology, crop or brand is best, such as Kirman [1993] and Ellison and Fudenberg
[1993,1995]. The links between emulation and social learning models needs further
exploration.
A second reason the replicator dynamic is of interest is because some of
its the properties of the replicator dynamic extend to classes of more general processes
that correspond to other sorts of learning or emulation. Samuelson-Zhang[1992] and
Hofbauer and Weibull [1995] have results along these lines, giving sufficient conditions
for a dynamic process to eliminate all strategies that are eliminated by iterated strict
dominance.
The focus of the remainder of the essay is individual level models, and
more specifically on variants of "fictitious play" in two players games This is
not a comprehensive survey and many relevant papers have been left out ).. Moreover, we
will suppose that players observe the strategies played by their opponents at the end of
each round. If the game has a non-trivial extensive form, this implies that players see
how opponents would have played at information sets that were not reached.
The first question a learning model must address is what individuals
know before the game starts, and what it is that they are learning about. Are they
learning about exogenous data and choosing best responses, or are they learning how to
play? A closely connected issue is how much rationality to attribute to the agents? We
believe that for most purposes the right models involve neither full rationality nor the
extreme naïveté of most stimulus-response models; "better" models have agents
consciously but perhaps imperfectly trying to get a good payoff.
In this essay we will simplify matters by assuming that players know the
extensive form of the game and their own payoff functions. They may or may not know their
opponents payoffs, but they are concerned with it only insofar as they can use it to
deduce how their opponents will play. In this setup the only thing players are learning
about from one iteration of the game to the next one is the distribution of strategies
used by opponents.
From this point of view, if players do have information about opponents'
payoffs they use it to form priors beliefs about how their opponents are likely to play.
For example, they might think it is unlikely that opponents will play strategies that are
dominated given the presumed payoff functions.
These two cases fit most laboratory experiments, but in other applications players might have less information. At the other extreme, players might not know anything about their opponents, so that players do not even know if they are playing a game, and are only aware of a subset of their own possible strategies. They might observe only the history of payoffs and their own strategies, and discover new strategies by experimentation or deduction. So far only the genetic algorithm model of learning (for example Holland [1975] has attempted to explore a setting like this.
There are several ways of modeling learning about opponents' strategies.
In the Bayes model of learning agents have priors, likelihood functions, and update
according to Bayes rule. Such agents can be "Savage rational," but they need not
be fully rational in the sense of basing their inference on a correct model of the world.
Indeed, if correct model of the world means consistent with a common prior, then there the
issue of whether play converges to an equilibrium is moot, since play must be an
equilibrium (either Bayesian correlated, or Bayesian Nash) from the outset, as shown by
Aumann [1987], and Brandenburger and Dekel [1987]. So it is not sensible to impose a
common prior when trying to understand how learning leads to equilibrium.
Since we are trying to understand how common knowledge might arise from
common experience, and is not clear what we might mean by a model being correct without
common knowledge, we look at learning processes where the players' models of the
environment are "sensible" as opposed to "correct." (If we focus not
on players' models of the environment, but on the "behavior rules" by which they
choose their actions , then we are interested in sensible rules.) This means that players
are trying to get a good payoff. Moreover, sensible rules should do reasonably well in a
reasonably broad set of circumstances. Rules that do poorly even in simple environments
are not likely to be used for important decisions.
There are two levels of sophistication in learning. One is simply to
forecast how opposing players will play. However, if two people repeatedly play a two
person game against each other, they ought to consider the possibility that their current
play may influence the future play of their opponent. For example, players might think
that if they are nice they will be rewarded by their opponent being nice in the future, or
that they can teach their opponent to play a best response to a particular action by
playing that action over and over. Most of learning theory abstracts from these repeated
game considerations by explicitly or implicitly relying on a model in which the incentive
to try to alter the future play of opponents is small enough to be negligible. Lock-in
with small discount factors is one such model. A second class of models that makes
repeated play considerations negligible is that of a large number of players, who interact
relatively anonymously, with the population size large compared to the discount factor.
There are a variety of large-population models, depending on how players
meet, and what information is revealed at the end of each round of play.
Random Matching Model: Each period, all players are randomly matched. At
the end of each round each player observes only the play in his own match. The way a
player acts today will influence the way his current opponent plays tomorrow, but the
player is unlikely to be matched with his current opponent or anyone who has met the
current opponent for a long time. Myopic play is approximately optimal if the population
is finite but large compared to the discount factors. Most game theory experiments use
this design. Note, however, that myopic play need not be optimal for a fully rational
player (who knows that others play myopically) even in a large population if that player
is sufficiently patient; see Ellison [1995]).
Aggregate Statistic Model: Each period, all players are randomly
matched. At the end of the round, the population aggregates are announced. If the
population is large each player has little influence on the population aggregates, and
consequently little influence on future play, so players have no reason to depart from
myopic play. Some, but too few, experiments use this design.
Note that with either form of a large population, repeated game effects are small but not nonzero with the typical population size of 20 to 30 subjects. Since the aggregate statistic
model seems to approximate about as many real-world situations of
interest as the random-matching model, and has the additional virtue of promoting faster
learning, it is unfortunate that it has not been used more often. This may be due to a
fear that repeated game effects would prove larger in the aggregate statistic model, but
we are unaware of theoretical or empirical evidence that this is the case. Our guess is
that the preponderance of the random-matching model is due rather to the desire to
maintain comparability with past experiments.
Although the large population stories explain naïve or myopic play; they only apply if the relevant population is large. Such cases may be more prevalent than it first appears, as players may extrapolate between similar games. Most non-equilibrium models in the literature either explicitly or implicitly have a large population model in mind; Kalai and Lehrer [1993] is one notable exception.
Fictitious play is a kind of quasi-Bayesian model: Agents behave as if
they think they are facing an exogenous, stationary, unknown, distribution of opponents'
strategies. The standard formal model with a single agent in each player role. There is
some recent work by Kanivkoski and Young [1994] that examines the dynamics of fictitious
play in population of players.
In the standard formal model denote a strategy by player i by , and the set of available
strategies by
. As usual, we
will use
to denote the
player(s) other than i. The best response correspondence is denoted by
. In fictitious play, player i
has an exogenous initial weight function
. This weight is updated by adding 1 to the weight of each
opponent strategy each time it is played. The probability that player i assigns to player
-i playing
at date t is
given by
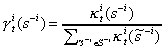
Fictitious play itself is then defined as any rule that assigns . This method corresponds to
Bayesian inference when player i believes that his opponents' play corresponds to a
sequence of i.i.d. multinomial random variables with a fixed but unknown distribution, and
player i's prior beliefs over that unknown distribution take the form of a Dirichlet
distribution.
Proposition (Fudenberg and Kreps 1993): (a) If s is a strict Nash
equilibrium, and s is played at date t in the process of fictitious play, s is played at
all subsequent dates. That is, strict Nash equilibria are absorbing for the process of
fictitious play. (b) Any pure strategy steady state of fictitious play must be a Nash
equilibrium. (c) If the empirical marginal distributions converge, the strategy profile
corresponding to the product of these distributions is a Nash equilibrium.
The early literature on fictitious play viewed the process as describing
pre-play calculations players might use to coordinate their expectations on a particular
Nash equilibrium (hence the name "fictitious" play.) From this viewpoint, or
when using fictitious play as a means of calculating Nash equilibria, the identification
of a cycle with its time average is not problematic, and the early literature on
fictitious play accordingly focused on finding conditions that guaranteed the empirical
distributions converge.
The convergence result above supposes players ignore cycles, even if, because of these cycles, the empirical joint distribution of the two players' play is correlated, and does not equal the product of the empirical marginals. Consider the following example, from Fudenberg and Kreps [1990], [1993]. (Similar examples can be found in Jordan [1993] and Young [1993])
| A | B | |
| A | 0,0 | 1,1 |
| B | 1,1 | 0,0 |
Suppose this game is played according to the process of fictitious play,
with initial weights (1, sqrt (2)) for each player. In the first period, both players
think the other will play B, so both play A. The next period the weights are (2,sqrt (2))
and both play B; the outcome is the alternating sequence ((B.,B),(A,A),(B,B), etc.) The
empirical frequencies of each player's choices do converge to 1/2, 1/2, which is the Nash
equilibrium, but the realized play is always on the diagonal, and both players receive
payoff 0 in every period. The empirical joint distribution on pairs of actions does not
equal the product of the two marginal distributions, so that the empirical joint
distribution corresponds to correlated as opposed to independent play. As a model of
players learning how their opponents behave, this is not a very satisfactory notion of
"converging to an equilibrium." Moreover, even if the empirical joint
distribution does converge to the product of the empirical marginals, so that the players
will end up getting the payoffs they would expect to get from maximizing against i.i.d.
draws from the long-run empirical distribution of their opponents' play, one might still
wonder if players would ignore persistent cycles in their opponents play.
One response to this is to use a more demanding convergence notion, and
only say that a player's behavior converges to a mixed strategy if his intended actions in
each period converge to that mixed strategy. The standard fictitious play process cannot
converge to a mixed strategy in this sense (for generic payoffs). Another response is to
think that fictitious play does describe the long-run outcome, and players will not notice
that their fictitious play model is badly off, provided that their payoffs are not worse
than the model predicts.
Fudenberg and Levine [1994] and Monderer, Samet, and Sela [1994] show that the realized time-average payoffs under fictitious play cannot be much below what the players expect if the time path of play exhibits "infrequent switches."
We now wish to contrast fictitious play with the partial best-response
model of learning in a large population. The partial adjustment model has a state variable
giving the fractions of the
population playing each
. In
discrete time, if a fraction of the population
is picked at random switch to the best response to their opponents
current play, and the rest of the population continues their current play, the partial
best-response dynamic is given by
.
If the time periods are very short, and the fraction of the population adjusting is very small, this may be approximated by the continuous time adjustment process
.
In contrast, the fictitious play process moves more and more slowly over
time, because the ratio of new observations to old observations becomes smaller and
smaller. Let denote the
historical frequency with which strategies have been played at time t. Then in fictitious
play
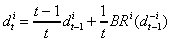
This is of course very much like the partial best-response dynamic, except that the weights on the past is converging to one, and the weight on the best response to zero.
Discrete-time fictitious play asymptotically approximately shares the
same limiting behavior as the continuous time best-response dynamic. More precisely, the
set of limit points of discrete time fictitious play is an invariant subset for the
continuous time best- response dynamics, and the path of the discrete-time fictitious play
process starting from some large T remains close to that of the corresponding continuous
time best- response process until some time , where
can be made arbitrarily large by taking T arbitrarily large. This was shown
by Hofbauer [1995].
In fictitious play, players can only randomize if exactly indifferent;
they cannot learn to play mixed strategies. To develop a sensible model of learning to
play mixed strategies, one should start with an explanation for mixing. One such
explanation is Harsanyi's [1973] purification theorem, which explains a mixed distribution
over actions as the result of unobserved payoff perturbations.
A second explanation for mixing is that it is descriptively realistic:
some psychology experiments show that choices between alternatives that are perceived as
similar tend to be relatively random.
A third motivation for supposing that players randomize is that
stochastic fictitious play allows behavior to avoid the discontinuity inherent in standard
fictitious play; consequently it allows much good long-run performance in a much wider
range of environments.
All three motivations lead to models where the best response function are replaced by "smooth best
response functions"
,
with
The notion of a Nash equilibrium in games with smoothed best response
functions is
Definition: The profile is a Nash distribution if
for all i.
This distribution may be very different from any Nash equilibria of the
original game if the smoothed best response functions are very far from the original ones.
But in the context of randomly perturbed payoffs, Harsanyi's purification theorem shows
that ("generically") the Nash distributions of the perturbed game approach the
Nash equilibria of the original game as the support of the payoff perturbations become
concentrated about 0.
The smoothed best-response function for the game of matching pennies is shown below
The "threshold perception" literature in psychology literature
shows that when asked to discriminate between two alternatives, behavior is random,
becoming more reliable as the alternatives become more distinct. In choosing between two
different strategies, one measure of the distinctness of the strategies is the difference
in utility between the strategies. With this interpretation, Thurstone's [1927] law of
comparative judgment becomes similar to Harsanyi's random utility model. Indeed, the
picture of the smooth best response curve drawn above is very similar to behavior curves
that have been derived empirically in psychological experiments.
While smooth fictitious play is random, the time average of many independent random variables has very little randomness. Asymptotically the dynamics resembles that of the continuous time "near best response" dynamics
.
Consequently, if the stochastic system eventually converges to a point
or a cycle, the point or cycle should be a closed orbit of the continuous-time dynamics.
Moreover, if a point or cycle is an unstable orbit of the continuous time dynamics, we
expect that the noise would drive the system away, so that the stochastic system can only
converge to stable orbits of the continuous-time system.
The literature on "stochastic approximation" gives conditions that allow the asymptotic limit points of stochastic discrete-time systems to be inferred from the stability of the steady states of a corresponding deterministic system in continuous time.
Proposition: (Benaim and Hirsch [1996]) Consider a two-player smooth
fictitious play in which every strategy profile has positive probability at any state . If
is an asymptotically stable equilibrium of the
continuous time process, then regardless of the initial conditions
.
Definition: A rule is
-universally
consistent if for any
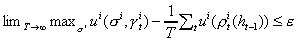
In words, using as the criterion the time average payoff, the utility
realized cannot be much less than that from the time invariant strategy.
This objective differs from the Bayesian approach of specifying prior
beliefs about strategies used by opponents choosing a best response to those beliefs.
However, any Bayesian expects to be consistent almost surely.
Existence of such rules originally shown by Hannan [1957], and by
Blackwell [1956]. The result has been lost and rediscovered several times since then by
many authors. In the computer science literature this is called the "on-line decision
problem."
Fudenberg and Levine [1995] show that universal consistency can be
accomplished by a smooth fictitious play procedure in which is derived from maximizing a function of the form
, and at each date players play
applied to their current
beliefs. For example, if
, then
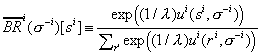
This is "exponential fictitious play": each strategy is played
in proportion to an exponential function of the utility it has historically yielded; it
corresponds to the logit decision model that has been extensively used in empirical work.
Notice that as the
probability that any strategy that is not a best response is played goes to zero.
Note also that this is not a very complex rule. Since it is not difficult to implement universally consistent rules universal consistency may be a useful benchmark for evaluating learning rules, even if it is not exactly descriptive of experimental data in moderate size samples and even if individual players do not implement the particular procedures discussed here.
The stimulus-response model was developed largely in response to observations by psychologists about human behavior and animal behavior: choices that lead to good outcomes are more likely to be repeated
behavior is random. All of these properties are shared by many learning
processes. Stimulus-response has received a fair bit of recent attention, but we fell that
researchers would do better to investigate models more in the style of smooth fictitious
play.
First consider stimulus response with only positive reinforcements, as
in Borgers-Sarin [1994]. Agents at each date use a mixed strategy, and the state of the
system is the vector of
mixed actions played at time t. Payoffs are normalized to lie between zero and one, so
that they have the same scale as probabilities. The state evolves in the following way: if
player i's payoff at date t is
, then
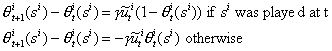
Because all payoffs are nonnegative, the propensity to play any action
increases each time that action is played.
Narendra and Thatcher [1974] showed that against an i.i.d. opponent, as
the reinforcement parameter goes
to zero, the time average utility converges to the maximum that could be obtained against
the distribution of opponents play. But this weak property is satisfied by many learning
rules that are not consistent, including "pure" fictitious play; smooth
fictitious play retains its consistency property regardless of opponents play.
Borgers-Sarin [1995] consider a more general model in which
reinforcements can be either positive or negative, depending on whether the realized
payoff is greater or less than the agent's "aspiration level." The simplest case
is a constant but nonzero aspiration level: if the aspiration level is greater than 1,
(all outcomes are disappointing) play cannot lock on to a pure action. Less obviously, if
there are only two strategies H and T, all payoff realizations are either 0 or 1, the
probability that H yields 1 is p, and the probability that T yields 1 is 1-p, ( as if the
agent is playing against an i.i.d. strategy in the game matching pennies) and the
aspiration level is constant at ½, then probability of playing H converges to p. This is
referred to as probability matching. This is not optimal, but at one time psychologists
believed it was characteristic of human behavior; we do not believe that they still do.
Roth and Er'ev [1994],[1996] develop a closely related but more highly
parameterized variation of the stimulus-response model and use it to study experimental
data on 2-player matrix games with mixed-strategy equilibria. They assume that the
aspiration level follows a linear adjustment process that ensures that the system moves
away from probability matching in the long run, and add a minimum probability on every
strategy. Their motivation is to see how far they can get with a "simple" model
with low cognition.
They have the nice idea of looking at experiments with very long run
length. This is important because learning theory suggests that many more trials are
needed for players to learn the distribution of opponents' play when it corresponds to a
mixed strategy than when it corresponds to a pure one.
The Roth and Er'ev model fits the aggregate data (pooled over subjects)
well, but it has a large number of free parameters. Most learning models with enough
flexibility in functional form are going to fit the aggregate data relatively well,
because of its high degree of autocorrelation.
Roth and Er'ev compare their stimulus-response model to a simple
(0-parameter) deterministic fictitious play on individual data, and argue that this
comparison makes a "case for low-rationality game theory." In my opinion, this
case is far from proven: they looked only at deterministic fictitious play, and we would
expect a priori that a deterministic model will not fit the individual data nearly as well
as a stochastic one. (This is acknowledged in Roth and Er'ev [1996], who say that
stochastic modifications of fictitious play are beyond the scope of the paper.) Also,
Er'ev and Roth specify a fictitious play with zero prior weights, which implies that the
players will be very responsive to their first few observations, while actual behavior is
known to be more "sluggish" than that.
In contrast, Cheung and Friedman [1994] have had some success in fitting
modified fictitious play models to experimental data. Their model (in games with 2
actions) has three parameters per player: the probability that a player uses his first
action is a linear function (2 parameters) of the exponentially-weighted history (1 more
parameter for the exponential weight.) The median exponential weighting over players and
experiments is about .3 or .4; best response corresponds to weight zero and classic
fictitious play is weight one.
Reflecting on these papers suggests to us that, as a group, theorists and experimenters should develop, characterize, and test models of "intermediate-cognition" procedural rationality; by this we mean models in which players are trying to maximize something in an approximate or loosely interpreted sort of way.
A simple experiment shows that prior information can have an important
impact on the course of play. This is the Prasnikar and Roth [1992] experiment on the
"best-shot" game, in which two players sequentially decide how much to
contribute to a public good. The backwards-induction solution to this game is for player 1
to contribute nothing and player 2 to contribute 4; there is also an imperfect Nash
equilibrium in which player 1 contributes 4 and player 2 contributes nothing. There is no
Nash equilibrium where player 1 mixes.
Prasnikar and Roth ran two treatments of this game. In the first,
players were informed of the function determining opponents' monetary payoffs. Here, by
the last few rounds of the experiment the first movers had stopped contributing. In the
second treatment, subjects were not given any information about the payoffs of their
opponents. In this treatment even in the later rounds of the experiment a substantial
number of player 1's contributed 4 to the public good, while others played 0.
This is not consistent with backwards induction or even Nash
equilibrium, but it is consistent with an (approximate, heterogeneous) self-confirming
equilibrium (Fudenberg and Levine [1996]). These experiments provide evidence that
information about other players' payoffs is used as if players maximized.
Aumann, R. [1987]: "Correlated Equilibrium as an Extension of Bayesian Rationality," Econometrica, 55:1-18.
Benaim, M. and M. Hirsch [1994]: "Learning Processes, Mixed Equilibria and Dynamical Systems Arising from Repeated Games".
Binmore, K. and L. Samuelson [1995]: "Evolutionary Drift and Equilibrium Selection," University College London.
Blackwell, D. [1956]: "Controlled Random Walks," Proceedings International Congress of Mathematicians, III 336-338, Amsterdam, North Holland.
Bjornerstedt, J. and J. Weibull [1995]: "Nash Equilibrium and Evolution by Imitation," in The Rational Foundations of Economic Behavior, (K. Arrow et al, ed.), Macmillan.
Borgers, T. and R. Sarin [1994]: "Learning through Reinforcement and the Replicator Dynamics," mimeo.
Brandenburger and E. Dekel [1987]. "Rationalizability and Correlated Equilibria," Econometrica, 55:1391-1402.
Cheung, Y. and D. Friedman [1994]: "Learning in Evolutionary Games: Some Laboratory Results," Santa Cruz.
Ellison, G. [1995] "Learning from Personal Experience: On the Large Population Justification of Myopic Learning Models," mimeo, MIT.
Ellison, G. and D. Fudenberg [1993] "Rules of Thumb for Social Learning," Journal of Political Economy 101:612-623.,
Ellison, G. and D. Fudenberg [1995] "Word of Mouth Communication and Social Learning," Quarterly Journal of Economics, 110:93-126.
Er'ev, I. and A. Roth [1996] "On The Need for Low Rationality Cognitive Game Theory: Reinforcement Learning in Experimental Games with Unique Mixed Strategy Equilibria," mimeo, University of Pittsburgh.
Fudenberg, D. and D. Kreps [1990]: "Lectures on Learning and Equilibrium in Strategic-Form Games," CORE Lecture Series.
Fudenberg, D. and D. Kreps[1993] "Learning Mixed Equilibria," Games and Economic Behavior 5, 320-367.
Fudenberg, D. and D. K. Levine [1994]: "Consistency and Cautious Fictitious Play," Journal of Economic Dynamics and Control, 19, 1065-1090.
Fudenberg, D. and D. K. Levine [1996] "Measuring Subject's Losses in Experimental Games," mimeo. UCLA.
Hannan, J. [1957]: "Approximation to Bayes Risk in Repeated Plays," in M. Dresher, A.W. Tucker and P. Wolfe, eds. Contributions to the Theory of Games, volume 3, 97-139, Princeton University Press.
Hofbauer, J. [1995] "Stability for the Best Response Dynamic," mimeo.
Hofbauer, J. and J. Weibull [1995]: "Evolutionary Selection against dominated strategies," mimeo, Industriens Utredningsintitut , Stockholm.
Holland, J.H. [1975] Adaptation in Natural and Artificial Systems, Ann Arbor: The University of Michigan Press.
Jordan, J. [1993]: "Three problems in Learning Mixed-Strategy Nash Equilibria," Games and Economic Behavior 5, 368-386.
Kalai, E. and E. Lehrer [1993]: "Rational Learning Leads to Nash Equilibrium," Econometrica 61:1019-1045.
Kanivokski, Y. and P. Young [1994]: "Learning Dynamics in Games with Stochastic Perturbations," mimeo
Kirman, A. [1993]: "Ants, Rationality and Recruitment," Quarterly Journal of Economics, 108, 137-156.
Monderer, D., D. Samet and A. Sela [1994]: "Belief Affirming in Learning Processes," Technion.
Narendra, K. and M. Thatcher [1974]: "Learning Automata: a Survey" IEEE Transactions on Systems, Man and Cybernetics , 4, 889-899.
Prasnikar V. and A. Roth [forthcoming]: "Considerations of fairness and strategy: experimental data from sequential games," Quarterly Journal of Economics.??
Roth A. and I. Er'ev [1994]: "Learning in Extensive-Form Games: Experimental Data nd Simple Dynamic Models in the Intermediate Term," Games and Economic Behavior, 8, 164-212.
Samuelson, L. and J. Zhang [1992]: "Evolutionary Stability in Asymmetric Games," Journal of Economic Theory , 57, 363-391.
Schlag, K. [1995]: "Why Imitate, and if so, How? Exploring a Model of Social Evolution," D.P. B-296, Universitat Bonn
Young, P. [1993]: "The Evolution of Conventions," Econometrica, 61, 57-83.