Based on a talk given at the Santa Cruz Conference on Sequence Prediction
David K. Levine
June 25, 1996
A canonical problem studied by game theorists is that of a strategic form game played repeatedly between randomly matched players. The random matching in a large population provides a rationale for the assumption that players play myopically when considering the effect that their current actions may have on the future play of opponents.
The criterion generally used in forecasting or learning theory is the quality of predictions that are made. In contrast, game theory more appropriately considers the utility that is derived from the learning rule.
The standard theory of learning used by game theorists is pretty primitive: usually it is some kind of variation of gradient dynamics, that is, a gradual adjustment in direction of increasing utility. An example of this type of dynamic is fictitious play. Ficitious play plays a best-response to the historical frequency of opponents' play. On a logarithmic time scale, in the long-run this is essentially the same thing as continuous adjustment in the direction of increasing utility.
As this is a talk for non-game theorists, I'll focus the remainder of the presentation on games that have proven of great importance to game theorists, games that raise some of the questions that we hope that learning theory might help us resolve.
The repeated prisoner's dilemma game is a two player game with payoffs given below
| 6,6 | 0,7 |
| 7,0 | 2,2 |
If this game is repeated (between the same players) a finite number of times, no matter what you think your opponent is going to do in the final round you should play down (or right). In the next to last round, you should anticipate this play by your opponent, and since he will play down (or right) no matter what you do now, again you should play down (or right). This "subgame perfection" argument implies that there should be a unique outcome of the game: down, right in every period. Yet both players would do better if they both play up and left (in economists terms, up and left pareto dominates down and right). In fact in experimental settings, up and right is frequently observed. This is a classic example of the "tragedy of the commons" that plays a central role in much of economics.
By way of contrast, if the game is infinitely repeated with relatively patient players, the "folk theorem" says that every payoff vector that gives each player an average utility per period of at least 2 and that is socially feasible can be realized by means of a "subgame perfect" equilibrium. For example, the strategies of play up (or left) in the first period, and continue to do so as long as your opponent has played left (or up), then revert to down (or right) forever afterwards is an equilibrium provided that the gain of 1 unit of utility for a single period is less than the loss of 4 units of utility per period forever after. On the other hand playing down (or right) every period is also an equilibrium.
This vast multiplicity of equilibria with infinite horizon is of great concern to game theorists. Can learning theory tell us something about which equilibrium we are likely to see when there are many equilibria?
A simpler setting in which to study the problem of multiple equilibria is the coordination game below.
| 2,2 | 1,1 |
| 1,1 | 2,2 |
This game (when played a single time) has three equilibria: up-left, down-right and a mixed equilibrium in which both players randomize with equal probability of up-down (or left-right). This gives each player an expected utility of 1 ½ .
Without some sort of common history or other coordinating device, the mixed equilibrium seems the most plausible. Consider however, the game
| 3,3 | 1,1 |
| 1,1 | 2,2 |
Here we might expect that both players would play up (or left), since this is clearly better for both players, and there is no conflict in objective.
An even more interesting example is the game
| 4,4 | 0,2 |
| 2,0 | 3,3 |
This also has three equilibria, the outcome (4,4) which is pareto efficient, the mixed equilibrium in which the randomization is 3/5, 2/5 yielding utility 2 2/5 to each player, and the equilibrium outcome (3,3). This latter equilibrium at (3,3) is called "risk dominant." If you are unsure how the other player is going to play, you stand to lose only one unit of utility if you are wrong at the (3,3) equilibrium, while you will lose 4 at the (4,4) equilibrium. If you are uncertain, you may view playing down (or right) as the better choice.
Standard learning theory says that equilibria in which a player strictly loses by deviating are dynamically stable. However, if we introduce randomness that does not fade over time in 2x2 games we find that only the risk dominant equilibria survive.
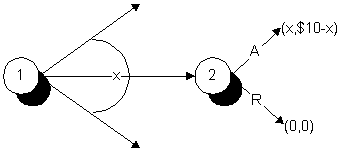
Another big puzzle for subgame perfection is the ultimatum bargaining game drawn below. Player 1 moves first and offers to divide ten dollars in a particular way. Player 2 may then either accept or reject the offer. If the offer is rejected, neither player gets anything.
Subgame perfection says that player 2 should be happy with anything he gets. As a result, player one should either demand the entire ten dollars, or at least $9.95 (offers must be made in nickles).
The table below reproduces data from a series of ultimatum bargaining experiments. These are typical of a large literature that has found similar results in a wide variety of experimental settings.
| x | cases | fraction of cases | Accepted Demands | Probability of Acceptance |
| $5.00 | 37 | 28% | 37 | 1.00 |
| $6.00 | 67 | 52% | 55 | 0.82 |
| $7.00 | 26 | 20% | 17 | 0.65 |
[from Roth, A., V. Prasnikar, M. Okuna-Fujiwara, S. Zamir [1991], "Bargaining and Market Behavior in Jerusalem, Ljubljana, Pittsburgh and Tokyo: An Experimental Study," American Economic Review, 81, 1068-1095.]
This is clearly inconsistent with subgame perfection. The puzzle is not so much in the behavior of player 1, since player 2's reject bad offers, it make sense not to be too demanding. What is puzzling is the rejection of a substantial number of decent (more than $3.00) offers by player 2's. Keep in mind, that in this experiment, play is anonymous, and you never play against the same player twice, and this is known to the subjects. So there is no reputation to uphold by rejecting a bad offer. However, this game illustrates an important limitation of learning theory: we can scarcely postulate that the problem is that the player 2's have not been able to learn that three dollars is better than none.